Ordinary PD controllers have a number of problems:
- If gains are high then they are usually unstable
- If gains are low then they converge slowly
- If damping is low, they converge quickly but overshoot the target and oscillate
- If damping is high then they converge slowly
- Tweeking gains is tedious and error prone
Stable Proportional Derivative Controllers (SPD) (See Paper) eliminate these problems. They converge very quickly. Look at this example. Notice that the SPD controller starts to decelerate the cube before it reaches the target.

A normal PD controller calculates the force to apply using:
f = -kp * (p – pTarg) – kd * (v – vTarg)
Where p and v values are the current rigidbody state from the current timestep. The PD controller keeps accelerating the body toward its target, even if it is on a trajectory that will overshoot.
SPD changes this by using this:
f = -kp * (p1 – pTarg1) – kd * (v1 – vTarg1)
Where p1 and v1 values are the rigidbody state from the next timestep. Since we don’t know the state of the body in the future. We estimate the state at the next timestep using the first term of a Taylor series.
- pTarg1 = pTarg0 + dt * vTarg0
- p1 = p0 + dt * v0
- vTarg1 = vTarg0
- v1 = v0 // assume v is constant because we don’t know
- f = -kp * (p1 – pTarg1) – kd * (v1 – vTarg1)
By looking where the body will be at the next timestep, the SPD controller can see that the body will overshoot the target. It is smart enough to start decelerating the body so that it is much more likely to align with the target values instead of overshooting. The result is a stable controller that converges very fast, and is fairly tolerant of a wide range of gains.
According to the paper the controller is stable if:
- kd ≥ kp * dt
In practice, using a game physics engine, it is also best not to apply truly gigantic forces and torques to your Rigidbodies.
Here is an example of the controller trying to track the rotation of a quaternion.
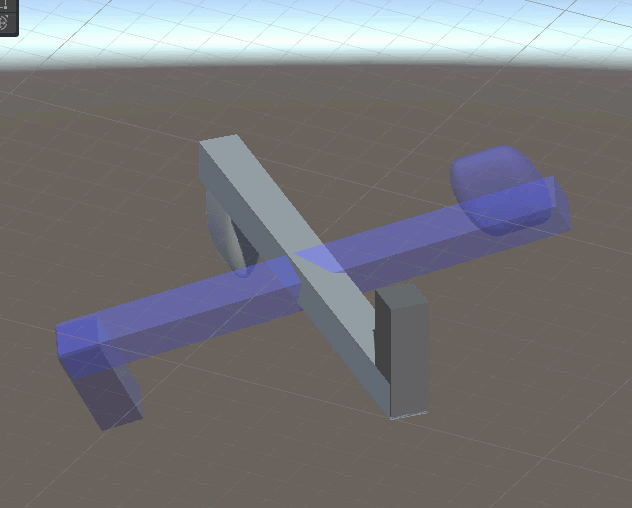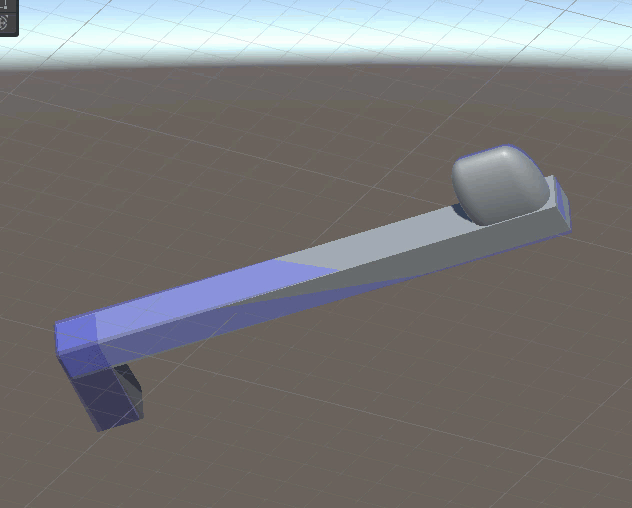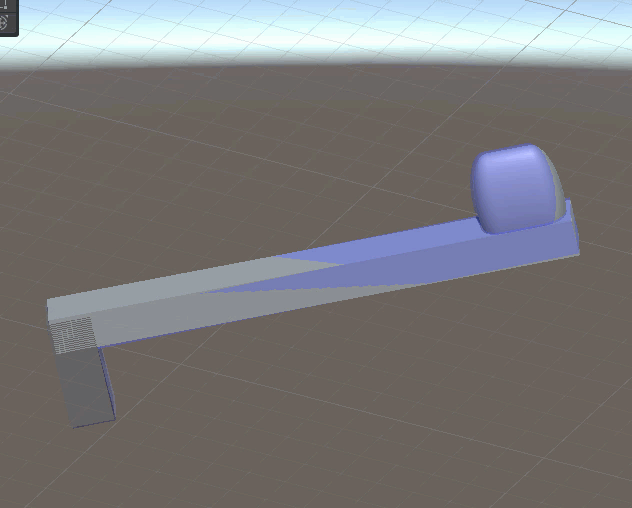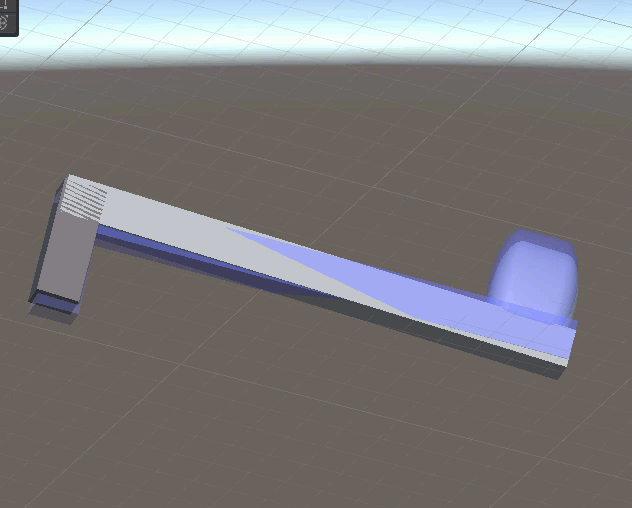
Here is a simple struct that computes acceleration or force using one dimensional linear SPD. To compute force instead of acceleration the acceleration is multiplied by the mass.
The code is available at github: https://github.com/Phong13/UsefulUtils
public struct SPDFloatCalculatorV2
{
public float kd;
public float kp;
public float mass;
public float dt;
public float ComputSPDAccelerationOnly(float p0, float v0,
float pTarg0, float vTarg0)
{
float pTarg1 = pTarg0 + dt * vTarg0;
float vTarg1 = vTarg0;
float p1 = p0 + dt * v0;
float a = -kp * (p1 - pTarg1) - kd * (v0 - vTarg1);
return a;
}
public float ComputSPDForce(float p0, float v0,
float pTarg0, float vTarg0)
{
float a = ComputSPDAccelerationOnly(p0, v0, pTarg0, vTarg0);
float f = mass * a;
return f;
}
}
Here is a quaternion version that computes an angular acceleration or torque. Computing the torque is more complicated by the need to transform the acceleration to and from the principal axis frame.
public struct SPDQuaternionCalculatorV2
{
public Vector3 inertiaTensor; // rigidbody.inertiaTensor
// rigidbody.intertiaTensorRotation
public Quaternion body_intertiaTensorRotation_dyn;
public float dt;
public float kp;
public float kd;
/// <summary>
/// V0 and vTarg0 are angular velocities.
/// They obey the left hand thumb rule in Unity.
/// </summary>
public Vector3 ComputSPDAccelerationOnly(Quaternion wld_Rot_p0, Vector3 v0_wld,
Quaternion wld_RotTarg_p0, Vector3 vTarg0_wld)
{
Quaternion wld_RotTarg_p1;
// = pTarg0 + dt * vTarg0
// expected body rotation one frame in the future.
{
float omegaTarg_rad = vTarg0_wld.magnitude;
if (omegaTarg_rad < 10e-8f)
{
wld_RotTarg_p1 = wld_RotTarg_p0;
}
else
{
Quaternion wld_delta_wld =
Quaternion.AngleAxis(omegaTarg_rad * dt * Mathf.Rad2Deg,
vTarg0_wld / omegaTarg_rad);
wld_RotTarg_p1 = wld_delta_wld * wld_RotTarg_p0;
}
}
Quaternion wld_Rot_p1;
// = p0 + _dt * v0;
// expected target rotation one frame in the future.
{
float omega = v0_wld.magnitude;
if (omega < 10e-8f)
{
wld_Rot_p1 = wld_Rot_p0;
}
else
{
Quaternion wld_delta_wld = Quaternion.AngleAxis(
omega * dt * Mathf.Rad2Deg,
v0_wld / omega);
wld_Rot_p1 = wld_delta_wld * wld_Rot_p0;
}
}
// p1 - pTarg1
// difference between current angle and target angle
float p_deltaMag;
Vector3 p_deltaDir_wld;
{
Quaternion wld_deltaP_wld = wld_Rot_p1 *
Quaternion.Inverse(wld_RotTarg_p1);
if (wld_deltaP_wld.w < 0f)
{
// The rotation is greater than 180 degrees
// (long way around the sphere).
// Convert to shortest path.
wld_deltaP_wld.x = -wld_deltaP_wld.x;
wld_deltaP_wld.y = -wld_deltaP_wld.y;
wld_deltaP_wld.z = -wld_deltaP_wld.z;
wld_deltaP_wld.w = -wld_deltaP_wld.w;
}
wld_deltaP_wld.ToAngleAxis(out p_deltaMag, out p_deltaDir_wld);
p_deltaDir_wld.Normalize();
p_deltaMag *= Mathf.Deg2Rad;
}
Vector3 a = -kp * p_deltaDir_wld * p_deltaMag - kd * (v0_wld - vTarg0_wld);
return a;
}
public Vector3 ComputSPDTorque(Quaternion wld_Rot_p0, Vector3 v0_wld,
Quaternion wld_RotTarg_p0, Vector3 vTarg0_wld
)
{
// acc_wld is the kinematic angular acceleration in wld frame.
// Calculated using SPD
Vector3 acc_wld = ComputSPDAccelerationOnly(wld_Rot_p0, v0_wld,
wld_RotTarg_p0, vTarg0_wld);
// Calc transform from world frame to objects principal axis frame
Quaternion wld_Rot_paxis = wld_Rot_p0 * body_intertiaTensorRotation_dyn;
// We need to convert the acceleration to
// torque in the principal axis frame.
// In this frame the inertia matrix is diagonal.
// The inertiaTensor vector is the
// non-zero diagonal entries of this matrix.
Vector3 acc_paxis = Quaternion.Inverse(wld_Rot_paxis) * acc_wld;
// Now that we are in dynamics principal axis frame,
// we can compute torque using:
// torque = intertiaTensor * angularAcceleration
Vector3 torque_dyn;
torque_dyn.x = inertiaTensor.x * acc_paxis.x;
torque_dyn.y = inertiaTensor.y * acc_paxis.y;
torque_dyn.z = inertiaTensor.z * acc_paxis.z;
// Now transform the torque from principal axis frame back to world frame.
Vector3 torque_wld = wld_Rot_paxis * torque_dyn;
return torque_wld;
}
}